RSA科普——大质数与指数选取

       如何生成这两个大质数，这是个值得研究的问题。首先可以想到的是生成质数序列，从中随机选取2个大质数即可。一种改进的方法是: 除了 2 外的偶数肯定不是质数，而奇数可能是质数，可能不是，那就可以跳过2与3的倍数，即对于 6n，6n+1, 6n+2, 6n+3, 6n+4, 6n+5，我们只需要判断 6n+1 与 6n+5 是否是质数即可。而判断某个数m是否是质数，最基本的方法就是对 2 到 m-1 之间的数除 m，如果有一个数能够整除 m，则 m 就不是质数。判断 m 是否是质数还可以进一步改进，只需要对 2 到根号√m之间的数除 m 就可以。继续优化，其实只用 2 到√m之间的质数去除即可。上面生成大质数是很基础的方法，效率比较低，一般会采用更快的方式，比如随机生成一个 nbits 位的奇数 p，然后从 p 开始遍历之后的奇数，并通过Miller–Rabin 质数判定算法对遍历到的数字进行质数判定，如果是质数，即可返回(当然，该算法有一定的误判率，不过在判定次数设置够大的情况下，误判率基本可以忽略)。

在选用公钥指数时，人们普遍会认为3和17没有65537安全。然而这种想法并没有合理的依据。实际上采用这三个值中的任何一个都不存在安全问题。前提是使用正确的填充方案。

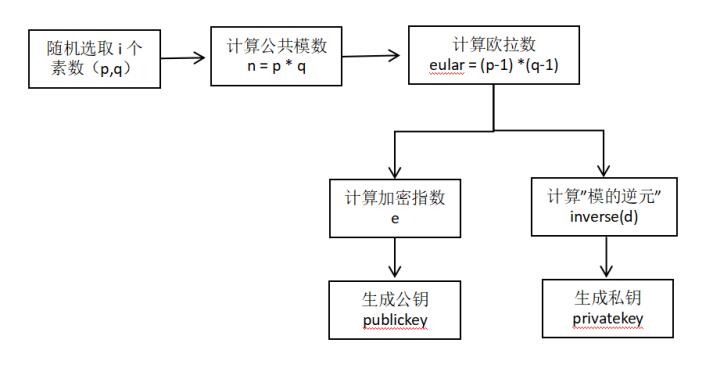
       (5)生成公钥、私钥。